Estudio y representación de funciones (con el uso de la derivada)
15 mayo, 2019

En el planteamiento de problemas típicos es frecuente manejar funciones matemáticas que describen los fenómenos y que conviene optimizar. Para ello se procede comúnmente al estudio (ver tabla resumen) de los puntos singulares de la función y al análisis de sus tendencias dentro de un marco concreto de valores.
Para estudiar una función:
- Lo primero que suele hacerse es determinar su dominio de definición, esto es, el conjunto de valores de la variable para los cuales la función toma valor real.
- Seguidamente se procede a estudiar la posible existencia de simetrías y periodicidades en la función, y se determinan los puntos de corte de la misma con los ejes, así como las asíntotas.
- Otro aspecto importante en el estudio de una función consiste en analizar sus tendencias de crecimiento o decrecimiento y extremos relativos. Y por último se estudiará la curvatura (concavidad-convexidad) de la función y sus puntos de inflexión.
- Una vez realizado este estudio preliminar, pasaremos a realizar una tabla resumen de puntos de la función y finalmente la gráfica de la misma.
Te presentamos ejemplos de un estudio completo de una función. Los casos más frecuentes y sencillos son los que tratan sobre funciones polinómicas y racionales. No obstante, en los enlaces de abajo puedes analizar otro tipo de funciones: irracionales, logarítmicas, exponenciales, trigonométricas, etc.


- 6 ejemplos resueltos de estudio y representación de funciones racionales (nivel medio)
- 7 ejemplos resueltos de estudio y representación de funciones racionales (nivel medio-alto)

- Resúmen teórico sobre el análisis o estudio de funciones
- Colección de ejercicios sobre análisis y representación de funciones con el uso de la derivada
![]()
- Estudio de monotonía y curvatura de una función polinómica (parte I)
- Estudio de monotonía y curvatura de una función polinómica (parte II)
- Estudio y gráfica de una función racional (27 min.)
- Análisis completo de una función racional (25 min.)

- Estudio y representación gráfica de todo tipo de funciones
1. Representación gráfica de funciones
2. Representación de funciones polinómicas
3. Representación de funciones racionales
4. Representación de funciones irracionales
5. Representación de funciones exponenciales
6. Representación de funciones logarítmicas
7. Representación de funciones trigonométricas
- Ejercicios y problemas
1. Representación de funciones polinómicas
2. Representación de funciones racionales I
3. Representación de funciones racionales II
4. Representación de funciones irracionales
5. Representación de funciones exponenciales
6. Representación de funciones logarítmicas
7. Representación de funciones trigonométricas I
8. Representación de funciones trigonométricas II
 Utilizando el
Utilizando el 







 t2 – 3t – 4 = 0luego se deshace el cambio de variable.
t2 – 3t – 4 = 0luego se deshace el cambio de variable.

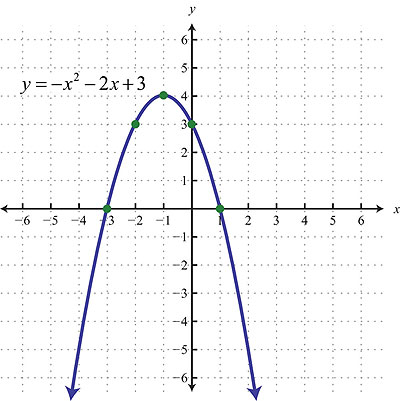

 La interpolación consiste en hallar un dato dentro de un intervalo en el que conocemos los valores en los extremos. Si se supone que las variaciones son proporcionales se utiliza la interpolación lineal.
La interpolación consiste en hallar un dato dentro de un intervalo en el que conocemos los valores en los extremos. Si se supone que las variaciones son proporcionales se utiliza la interpolación lineal. Despejando y2 obtenemos que:
Despejando y2 obtenemos que:









