 La programación lineal (PL) es un procedimiento o algoritmo matemático mediante el cual se resuelve un problema indeterminado, formulado a través de un sistema de inecuaciones lineales optimizando una función objetivo, también lineal.
La programación lineal (PL) es un procedimiento o algoritmo matemático mediante el cual se resuelve un problema indeterminado, formulado a través de un sistema de inecuaciones lineales optimizando una función objetivo, también lineal.
El matemático fránces Jean Baptiste-Joseph Fourier (1768-1830) fue el primero en intuir, aunque de forma imprecisa, los métodos de lo que actualmente llamamos programación lineal y la potencialidad que de ellos se deriva.
Como origen de la PL, en 1947, G.B. Dantzig formula, en términos matemáticos muy precisos, el enunciado estándar al que cabe reducir todo problema de programación lineal. Se trata de dar respuesta a situaciones en las que se exige maximizar o minimizar funciones (beneficios, costes, etc) que se encuentran sujetas a determinadas limitaciones, que llamaremos restricciones (nº de operarios, maquinaria, kg mercancía, etc) .
Su empleo es frecuente en aplicaciones de la industria, la economía, la estrategia militar, etc.
Existen tres métodos para resolver un problema de PL con dos variables (x,y):
Nosotros optaremos por explicar el segundo método, pues resulta más intuitivo y sencillo.

ETAPAS DEL MÉTODO DE LOS VÉRTICES APLICADO A LA PROGRAMACIÓN LINEAL
Los pasos a seguir son:
1 Elegir las incógnitas.
2 Escribir la función objetivo en función de los datos del problema.
3 Escribir las restricciones en forma de sistema de inecuaciones.
4 Averiguar el conjunto de soluciones factibles representando gráficamente las restricciones.
5 Calcular las coordenadas de los vértices del recinto de soluciones factibles (si son pocos).
6 Calcular el valor de la función objetivo en cada uno de los vértices para ver en cuál de ellos presenta el valor máximo o mínimo según nos pida el problema (hay que tener en cuenta aquí la posible no existencia de solución si el recinto no está acotado)
Función Objetivo
En esencia la programación lineal consiste en optimizar (maximizar o minimizar) una función objetivo, que es una función lineal de varias variables, en casos sencillos dos variables: f(x,y) = ax + by
Restricciones
La función objetivo está sujeta a una serie de restricciones, expresadas por inecuaciones lineales:
a1x + b1y ≤ c1
a2x + b2y ≤ c2
anx + bny ≤ cn
Cada desigualdad del sistema de restricciones determina un semiplano.
Región factible
El conjunto intersección, de todos los semiplanos formados por las restricciones, determina un recinto limitado o ilimitado, llamado región factible, acotado o no, que recibe el nombre de región de validez o zona de soluciones factibles.
Solución óptima
El conjunto de los vértices del recinto se denomina conjunto de soluciones factibles básicas y el vértice donde se presenta la solución óptima se llama solución máxima (o mínima según el caso).
Pulsa en este enlace para visualizar un ejemplo totalmente comentado que te ayudará a comprender este método.
Valor del programa lineal
El valor que toma la función objetivo en el vértice de solución óptima se llama valor del programa lineal.
CASOS DE EJERCICIOS QUE SE PUEDEN PRESENTAR
Los problemas de Programación Lineal con dos variables se pueden clasificar, atendiendo al tipo de solución que presentan, en:
- Factibles (con solución, por tanto, cuando existen uno más valores que satisfacen las restricciones)
- No factibles (sin solución, por tanto, cuando las restricciones son inconsistentes)
A su vez los casos factibles pueden ser de:
- Solución única
- Solución múltiple
- Solución no acotada (algunos casos en los que la región factible sea ilimitada)
 + INFO (MÉTODO DE PROGRAMACIÓN LINEAL)
+ INFO (MÉTODO DE PROGRAMACIÓN LINEAL)




 La función así obtenida es la inversa de la función dada.
La función así obtenida es la inversa de la función dada.


![]()


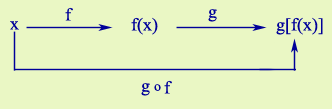

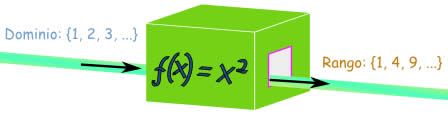
 , donde los dominios suelen aparecer como intervalos, inecuaciones o puntos.
, donde los dominios suelen aparecer como intervalos, inecuaciones o puntos.


 La
La 








 Para resolver una inecuación polinómica , seguiremos los siguientes pasos:
Para resolver una inecuación polinómica , seguiremos los siguientes pasos:








